近世代数

1.引入:

近世代数主要研究所谓的代数系统,即带有运算的集合；研究代数运算的规律和各种代数系统的性质。

2.基本概念:

2.1 二元运算:

s为集合,sxs到s的映射,成为s上的一个二元运算.

S中任何两个元素的运算结果都属于S，这个性质称为运算的封闭性. (后面常说S对某运算封闭).

实例:

2.2 一元运算:

s到s的映射.

表示:

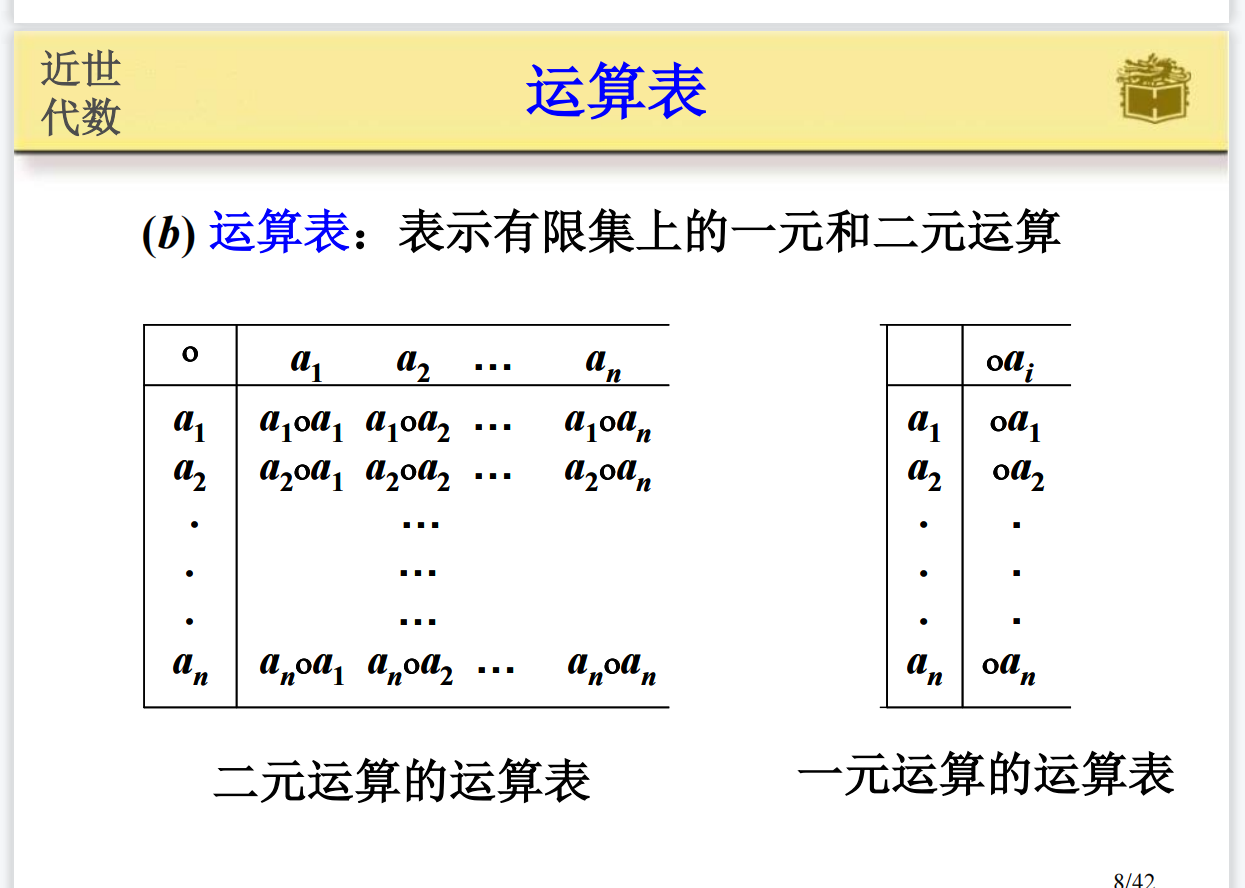
2.3 二元运算的规律:

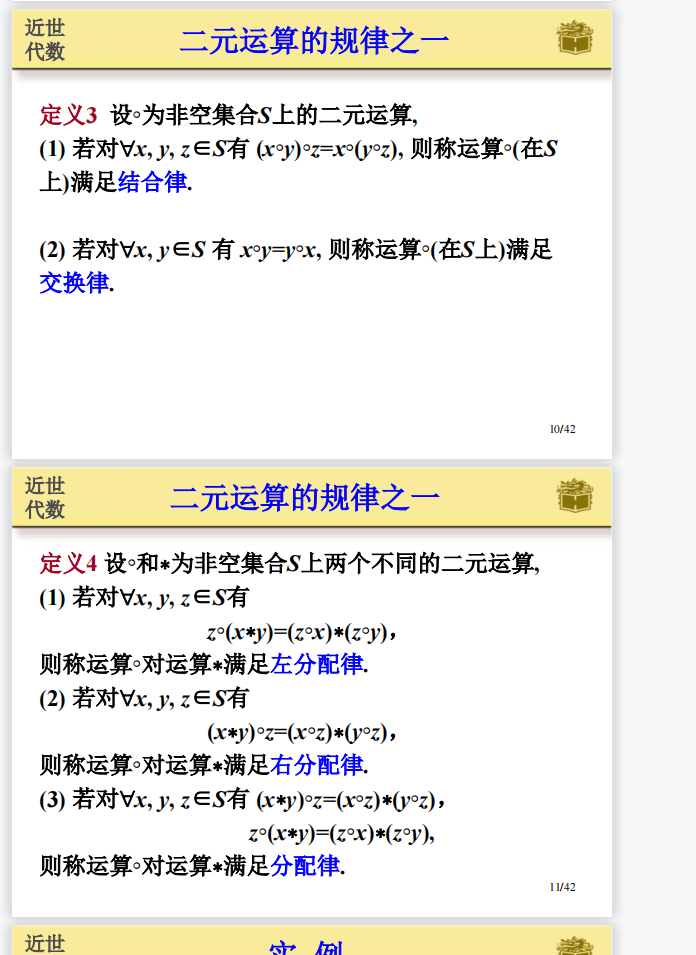
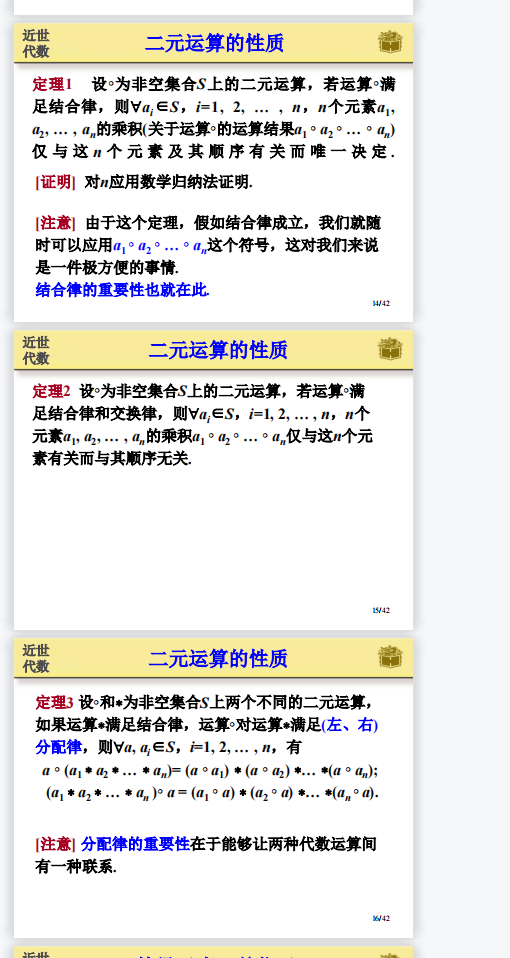
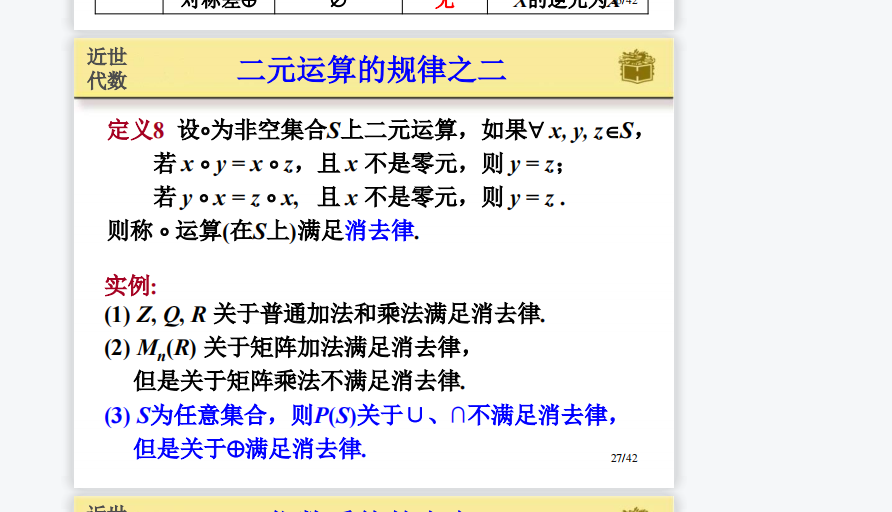
2.4 单位元:

类似乘法里面的1.

2.5 零元:

类似乘法中的0.

2.6 逆元:

类似倒数.

2.7 代数系统:

一个集合+集合上的一些二元运算.

近世代数（或抽象代数）的主要研究内容就是研究所谓的代数系统，即带有运算的集合。在近世代数里，不管是在群、环里还是在其它代数系统里，研究一种代数系统就是要解决这一系统的存在问题、数量问题和构造问题。如果对于一个代数系统，这三个问题能得到圆满的解答，研究的目的就算达到了 。

3.半群:

3.1 定义:

结合律:半群

交换律:交换半群,可换半群.

3.2 半群的术语:

单位元问题:

3.3 子半群:

3.4 理想:

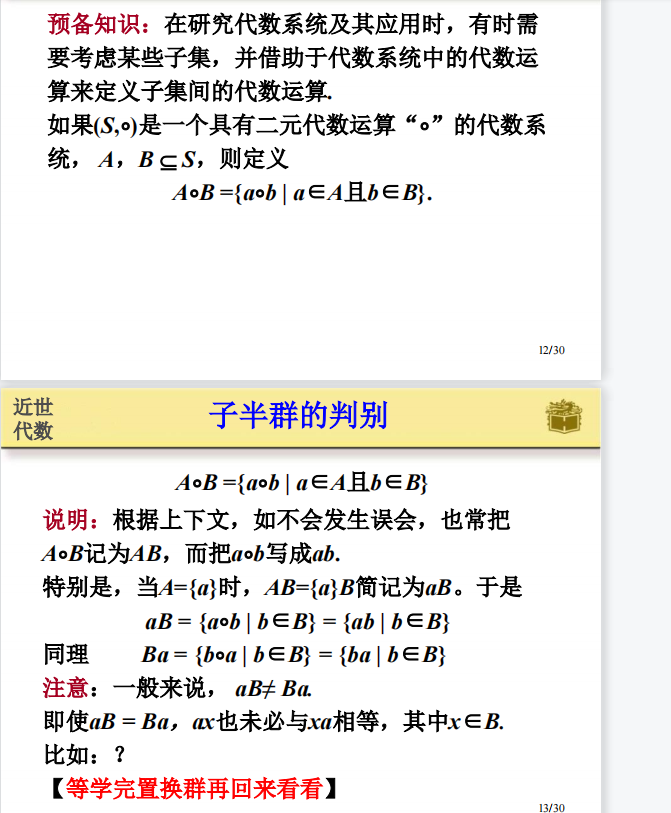
两个集合,不加符号,表示两个集合里面任意两个元素进行操作.

3.5 循环半群:

3.6 半群的同态和同构:

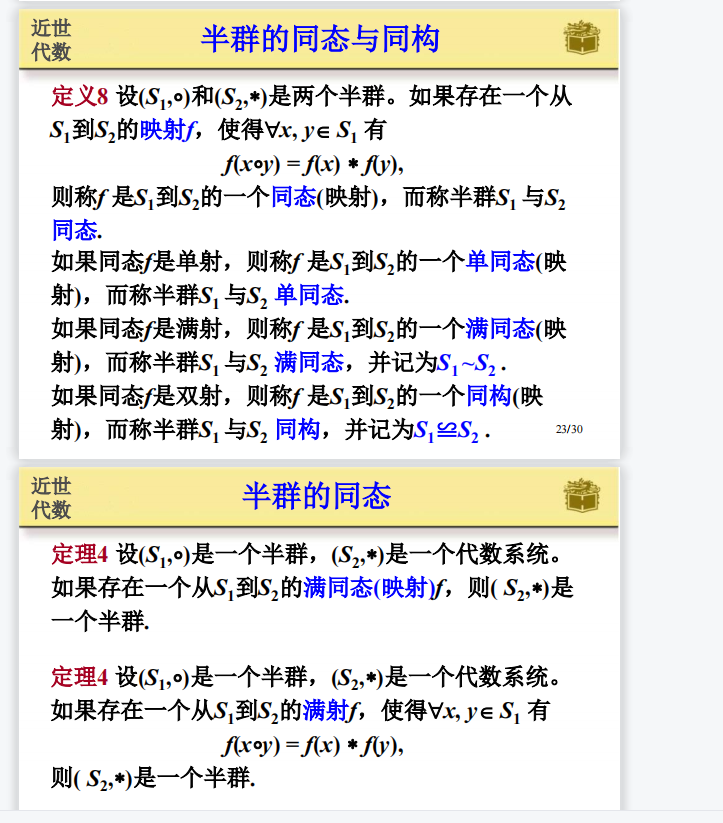
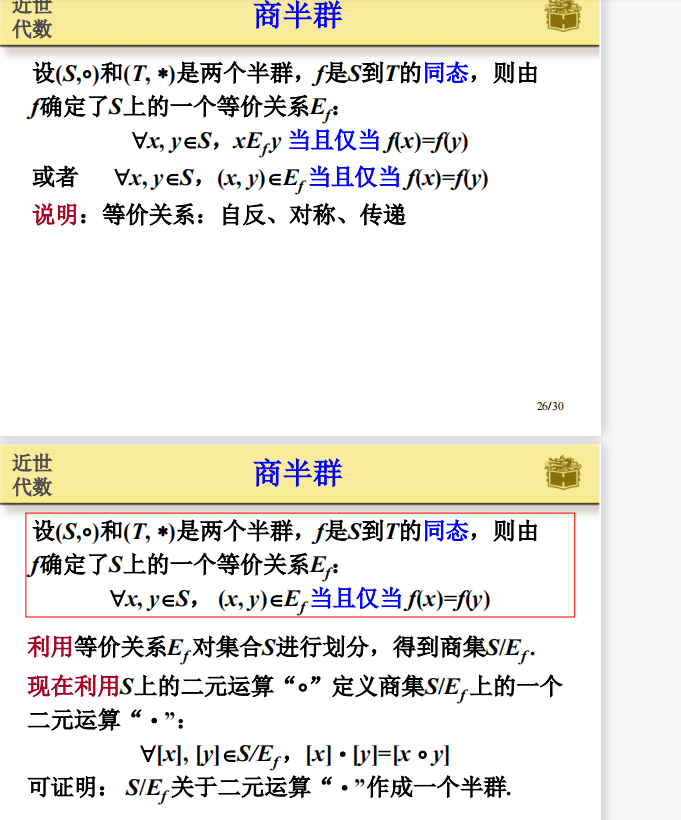
3.7 商半群:

4.幺半群:

有单位元的半群.

有单位元,符合集合律的代数系统.

4.1 幺半群的性质:

有限与无限. S集合的基数成为幺半群的阶.

有的有零元,有的没有零元.

4.2 逆元问题:

5.群:

5.1 定义:

6.有限群和子群:

在群的定义上加上有限集合的限制条件.

6.1 有限群的性质:

有限群的每个元素的阶均为有限且不超过群的阶.

6.2 子群的定义:

子集,运算封闭,构成群.

6.3 子群的性质:

判别子群的方法:

7.变换群:

7.1 变换:

7.2 变换群:

7.3 群的同构:

7.4 群的Cayley定理:

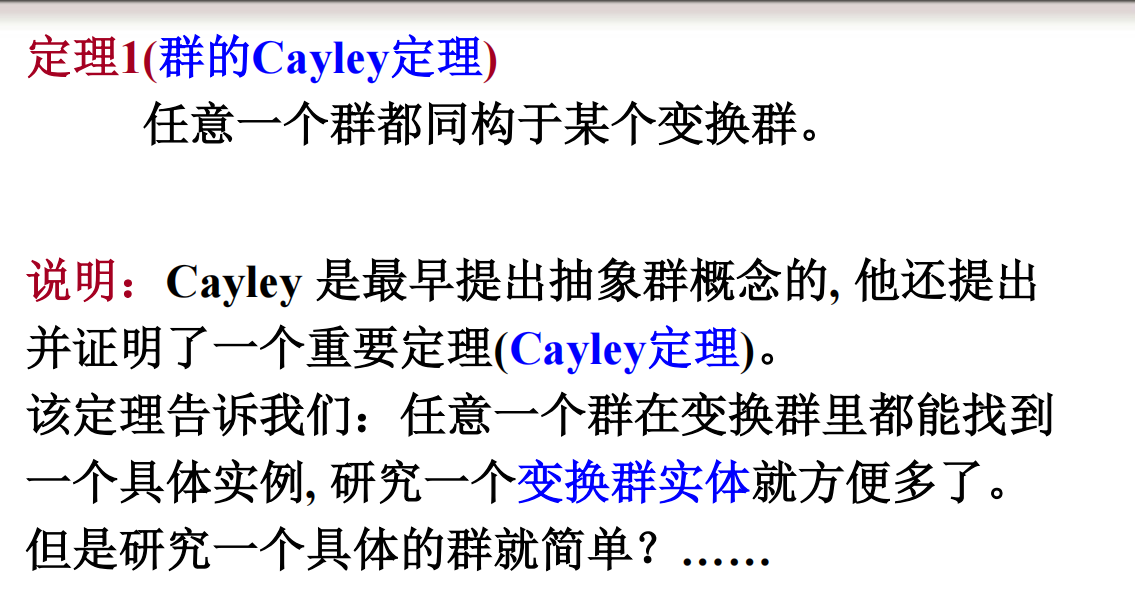
8.置换群:

8.1 定义:

特殊的变换群.

8.2 n元置换的乘法:

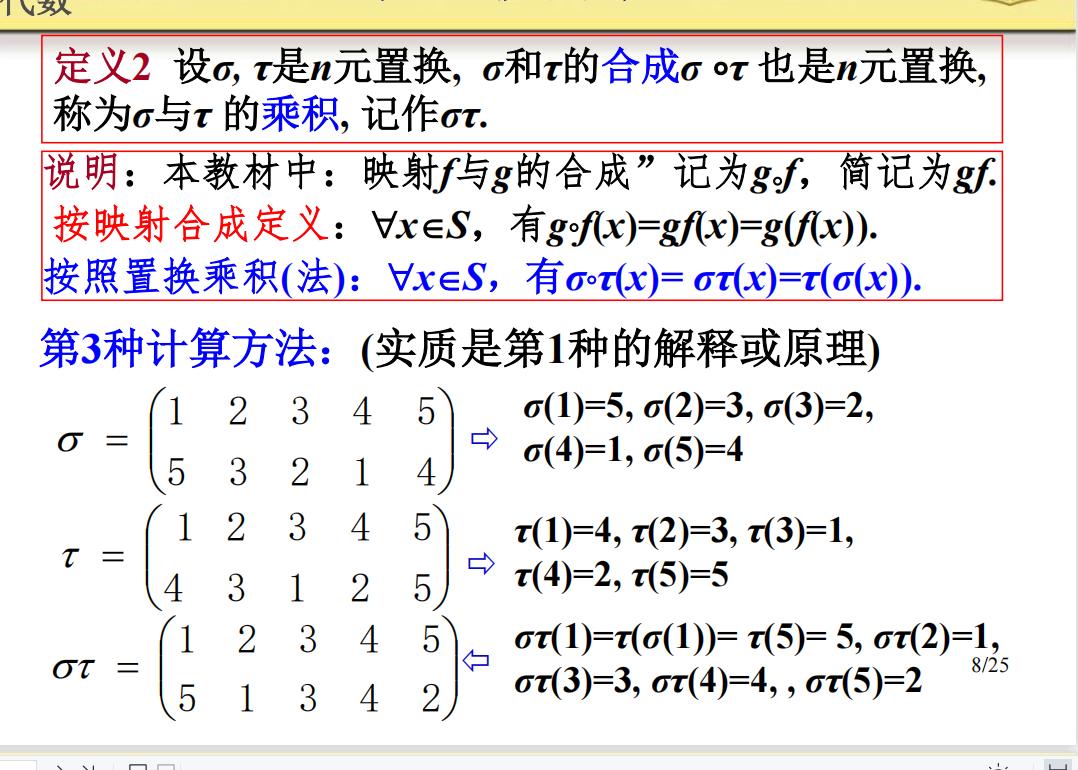
8.3 n元置换的性质:

8.4 置换群:

9.循环群:

9.1 定义:

循环群必定是交换群.

9.2 循环群的性质:

9.3 循环群的子群:

10. 子群的陪集:

10.1 陪集的定义:

10.2 左陪集的基本性质:

10.3 右陪集的基本性质:

10.4 陪集的基本性质:

10.5 Lagrange定理:

11. 群的同态基本定理:

11.1 正规子群与商群:

11.2 正规子群的判别定理:

12.环:

12.1 环的定义:

12.2 环的运算性质:

12.3 零因子:

12.4 特殊的环:

13.格:

13.1 定义:

偏序关系,自反,反对称,传递的关系称为偏序关系.

上确界:比两者都大,而却在这个偏序集中.符合这些条件的数里面最小的.

13.2 格的对偶原理:

13.3 格的性质:

13.4 格作为代数系统:

13.5 子格:

判别法:

13.6 格的同态和同构:

13.7 有界格:

补元:

13.8 分配格:

符合分配率的格.

性质:

14.布尔代数:

14.1 定义:

有补分配格称为布尔代数.

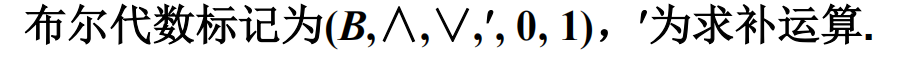
14.2 性质: