人工智能概论
本文最后更新于 2024-06-07,文章内容可能已经过时。
1. 绪论:
1.1 图灵测试:
图灵测试(The Turing Test)起源于计算机科学和密码学的先[艾伦·麦席森·图灵发表于1950年的一篇论文《计算机器与智能》。该测试的流程是,一名测试者写下自己的问题,随后将问题以纯文本的形式(如计算机屏幕和键盘)发送给另一个房间中的一个人与一台机器。测试者根据他们的回答来判断哪一个是真人,哪一个是机器。所有参与测试的人或机器都会被分开。这个测试旨在探究机器能否模拟出与人类相似或无法区分的智能 [1]。
现在的图灵测试测试时长通常为5分钟,如果电脑能回答由人类测试者提出的一系列问题,且其超过30%的回答让测试者误认为是人类所答,则电脑通过测试。
1.2 中国屋思考实验:

1.3 基本内容:
1.3.1 知识表示:
将人类知识形式化或者模型化。
1.3.2 机器感知:
使机器(计算机)具有类似于人的感知能力。以机器视觉(machine vision)与机器听觉为主。
1.3.3 机器思维:
对通过感知得来的外部信息及机器内部的各种工作信息进行有目的的处理。
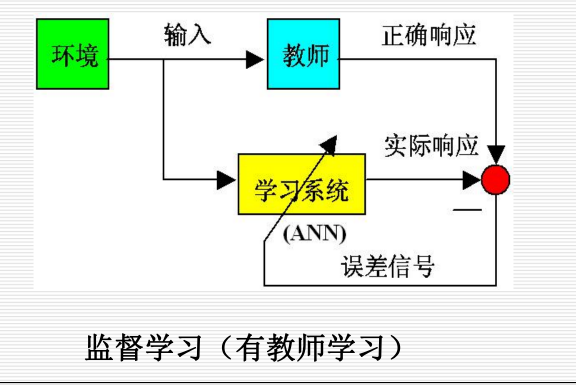
1.3.4 机器学习:
机器学习(machine learning):研究如何使计算机具有类似于人的学习能力,使它能通过学习自动地获取知识。
1.3.5 机器行为:
计算机的表达能力,即“说” 、 “写” 、“画”等能力。
2.知识表示和知识图谱:
2.1 知识表示:
2.1.1 特性:
2.1.1.1 相对正确性:
任何知识都是在一定的条件及环境下产生的,在这种条件及环境下才是正确的。
2.1.1.2 不确定性:
随机性引起的不确定性
模糊性引起的不确定性
经验引起的不确定性
不完全性引起的不确定性
2.1.1.3 可表示性与可利用性:
知识的可表示性:知识可以用适当形式表示出来,如用语言、文字、图形、神经网络等。
知识的可利用性:知识可以被利用。
2.2 一阶谓词逻辑表示法:
2.2.1 命题:
命题是一个非真即假的陈述句。
2.2.2 谓词:
谓词的一般形式: P (x1 , x2 ,…, xn)
某个独立存在的事物或者某个抽象的概念;

2.2.3 特点:

2.3 产生式:
2.3.1 分类:
确定性规则知识的产生式表示
不确定性规则知识的产生式表示
确定性事实性知识的产生式表示
不确定性事实性知识的产生式表示

2.4 产生式系统:
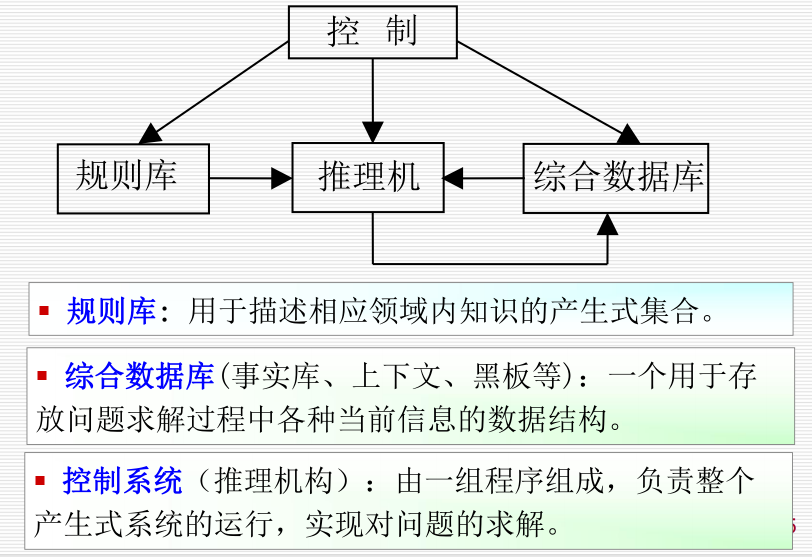
主要做以下工作:
(1)从规则库中选择与综合数据库中的已知事实进行匹配。
(2)匹配成功的规则可能不止一条,进行冲突消解。
(3)执行某一规则时,如果其右部是一个或多个结论,则
把这些结论加入到综合数据库中:如果其右部是一个或多个
操作,则执行这些操作。
(4)对于不确定性知识,在执行每一条规则时还要按一定
的算法计算结论的不确定性。
(5)检查综合数据库中是否包含了最终结论,决定是否停
止系统的运行。
2.5 框架表示法:
一种结构化的知识表示方法,已在多种系统中得到应用。
框架(frame):一种描述所论对象(一个事物、事件或概念)属性的数据结构。
一个框架由若干个被称为“槽”(slot)的结构组成,每一个槽又可根据实际情况划分为若干个“侧面”。(faced)。
一个槽用于描述所论对象某一方面的属性。一个侧面用于描述相应属性的一个方面。槽和侧面所具有的属性值分别
被称为槽值和侧面值。

2.6 知识图谱:
知识图谱是一种互联网环境下的知识表示方法。
知识图谱的目的是为了提高搜索引擎的能力,改善用户的搜索质量以及搜索体验。
知识图谱(Knowledge Graph/Vault),又称科学知识图谱,用各种不同的图形等可视化技术描述知识资源及其
载体,挖掘、分析、构建、绘制和显示知识及它们之间的相互联系。
知识图谱是由一些相互连接的实体及其属性构成的。三元组是知识图谱的一种通用表示方式:

2.6.1 架构:
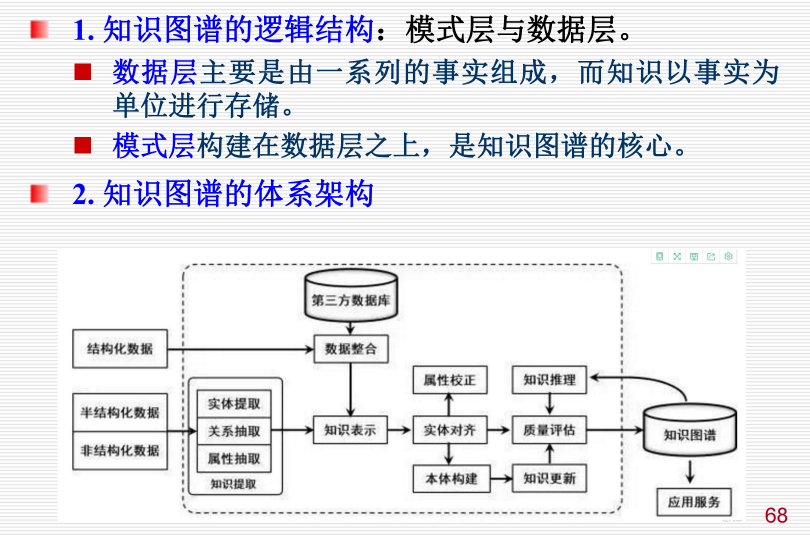
3.确定性推理方法:
推理是求解问题的一种重要方法。因此,推理方法成为人工智能的一个重要研究课题。
3.1 推理:
3.1.1 定义:
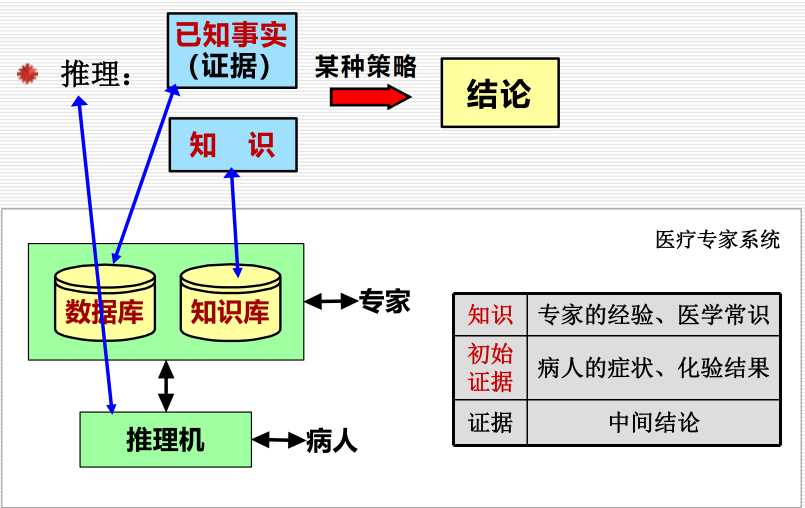
3.1.2 分类:
3.1.2.1 按照方式分类:
3.1.2.1.1 演绎推理:
演绎推理 (deductive reasoning) : 一般 → 个别

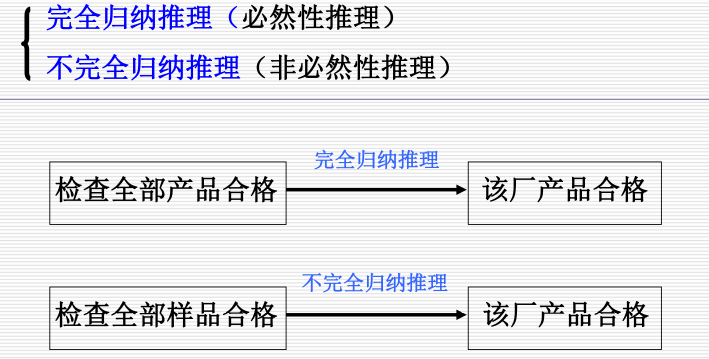
3.1.2.2.2 归纳推理:
归纳推理 (inductive reasoning): 个别 → 一般
3.1.2.3.3 默认推理:
默认推理(default reasoning,缺省推理)。
知识不完全的情况下假设某些条件已经具备所进行的推理。

3.1.2.4.4 确定推理/不确定推理:

3.1.2.5.5 单调式推理/非单调式推理:

3.1.2.6.6 启发式推理/非启发式推理:

3.1.3.2 按照方向分类:
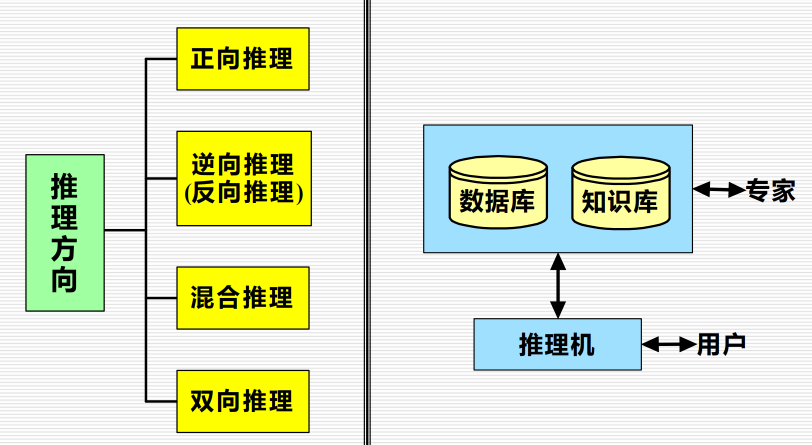
3.1.3.2.1 正向推理:
已知事实 → 结论
(1)从初始已知事实出发,在知识库KB中找出当前可适用的知识,构成可适用知识集KS。
(2)按某种冲突消解策略从KS中选出一条知识进行推理,并将推出的新事实加入到数据库DB中作为下一步推理已
知事实,再在KB中选取可适用知识构成KS 。
(3)重复(2),直到求得问题的解或KB中再无可适用的知识。
3.1.3.2.2 逆向推理:
以某个假设目标作为出发点
(1)选定一个假设目标。
(2)寻找支持该假设的证据,若所需的证据都能找到,则原假设成立;若无论如何都找不到所需要的证据,说明
原假设不成立的;为此需要另作新的假设。
3.1.3.2.3 混合推理:
(1)先正向后逆向:先进行正向推理,帮助选择某个目标,即从已知事实演绎出部分结果,然后再用逆向推理证
实该目标或提高其可信度;
(2)先逆向后正向:先假设一个目标进行逆向推理,然后再利用逆向推理中得到的信息进行正向推理,以推出更
多的结论。
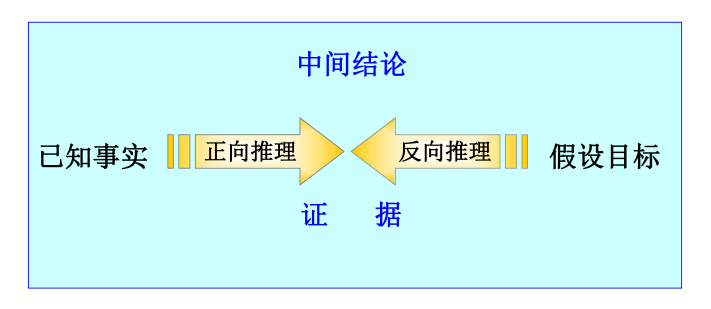
3.1.3.2.4 双向推理:
正向推理与逆向推理同时进行,且在推理过程中的某一步骤上“碰头”的一种推理。
3.1.3 冲突消解:

按针对性排序
按已知事实的新鲜性排序
按匹配度排序
按条件个数排序
3.2 自然演绎推理:
从一组已知为真的事实出发,运用经典逻辑的推理规则推出结论的过程。

表达定理证明过程自然,易理解。
拥有丰富的推理规则,推理过程灵活。
便于嵌入领域启发式知识。
4.不确定推理方法:
4.1 基本问题:
不确定性的表示与量度
不确定性匹配算法及阈值的选择
组合证据不确定性的算法
不确定性的传递算法
结论不确定性的合成
4.2 可信度方法:
可信度:根据经验对一个事物或现象为真的相信程度。
C-F模型:基于可信度表示的不确定性推理的基本方法。
4.2.1 表示:

4.3 证据理论:
证据理论(theory of evidence):又称D-S理论,是德普斯特(A. P. Dempster)首先提出,沙佛(G. Shafer)进
一步发展起来的一种处理不确定性的理论。
概率分配函数
信任函数
似然函数
概率分配函数的正交和(证据的组合)
基于证据理论的不确定性推理
4.4 模糊推理方法:
1965年,美国L. A. Zadeh发表了“fuzzy set”的论文,首先提出了模糊理论。
5.搜索求解策略:
在求解一个问题时,涉及到两个方面:一是该问题的表示,如果一个问题找不到一个合适的表示方法,就谈不上对
它求解。
另一方面则是选择一种相对合适的求解方法。由于绝大多数需要人工智能方法求解的问题缺乏直接求解的方法,因此,搜索为一种求解问题的一般方法。
5.1 状态空间搜索:
状态:表示系统状态、事实等叙述型知识的一组变量或数组:Q [ q 1 , q 2 , , q n ]
操作:表示引起状态变化的过程型知识的一组关系或函数:F { f 1 , f 2 , , f m }
状态空间:利用状态变量和操作符号,表示系统或问题的有关知识的符号体系,状态空间是一个四元组:( S , O , S
0 , G )
求解路径:从 S0 结点到 G 结点的路径。

5.2 盲目的图搜索策略:
5.2.1 回溯策略:
从初始状态出发,不停地、试探性地寻找路径,直到它到达目的或“不可解结点” ,即“死胡同”为止。
若它遇到不可解结点就回溯到路径中最近的父结点上,查看该结点是否还有其他的子结点未被扩展。若有,则沿这
些子结点继续搜索;如果找到目标,就成功退出搜索,返回解题路径。
(1) PS(path states)表:保存当前搜索路径上的状态。如果找到了目的,PS就是解路径上的状态有序集。
(2) NPS(new path state)表:新的路径状态表。它包含了等待搜索的状态,其后裔状态还未被搜索到,即未被
生成扩展 。
(3) NSS(no solvable states)表:不可解状态集,列出了找不到解题路径的状态。如果在搜索中扩展出的状态是
它的元素,则可立即将之排除,不必沿该状态继续搜索。
5.2.2 广度优先搜索:
每次选择深度最浅的节点首先扩展,搜索是逐层进行的;
一种高代价搜索,但若有解存在,则必能找到它。
5.2.3 深度优先搜索:
首先扩展最新产生的节点,深度相等的节点按生成次序的盲目搜索。
扩展最深的节点的结果使得搜索沿着状态空间某条单一的路径从起始节点向下进行下去;仅当搜索到达一个没有后
裔的状态时,才考虑另一条替代的路径。
5.3 启发式图搜索策略:
5.3.1 介绍:
用来简化搜索过程有关具体问题领域的特性的信息叫做启发信息。
启发式图搜索策略(利用启发信息的搜索方法)的特点:重排OPEN表,选择最有希望的节点加以扩展。
运用启发式策略的两种基本情况:
(1)一个问题由于存在问题陈述和数据获取的模糊性,可能会使它没有一个确定的解。
(2)虽然一个问题可能有确定解,但是其状态空间特别大,搜索中生成扩展的状态数会随着搜索的深度呈指数级
增长。
5.3.2 启发函数和估价函数:
估价函数(evaluation function):估算节点“希望”程度的量度。
从初始节点经过 n节点到达目标节点的路径的最小代价估计值,其一般形式是
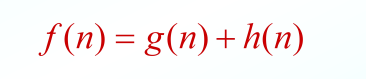
fn是估价函数 gn是实际代价函数 hn是启发函数
5.3.3 A搜索算法:
使用了估价函数 f 的最佳优先搜索。
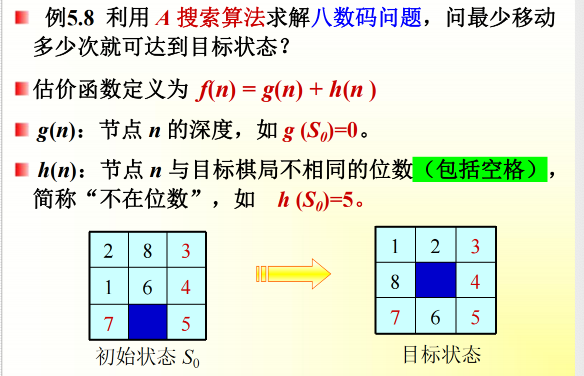
A搜索算法能不能保证找到最优解(路径最短的解)?不行。
5.3.4 A*搜索算法:
定义h*(n)为状态n到目的状态的最优路径的代价,则当A搜索算法的启发函数h(n)小于等于
h(n)时,即h(n)≤h(n),则被称为A*算法。
如果某一问题有解,那么利用A*搜索算法对该问题进行搜索则一定能搜索到解,并且一定能搜索到最优的解而
结束
6.智能计算及其应用:
智能优化方法通常包括进化计算和群智能等两大类方法,是一种典型的元启发式随机优化方法,已经广泛应用于组
合优化、机器学习、智能控制、模式识别、规划设计、网络安全等领域,是21世纪有关智能计算中的重要技一。
6.1 进化算法:
进化算法(evolutionary algorithms,EA)是基于自然选择和自然遗传等生物进化机制的一种搜索算法。
进化算法是一个“算法簇” ,包括遗传算法(GA)、遗传规划、进化策略和进化规划等。
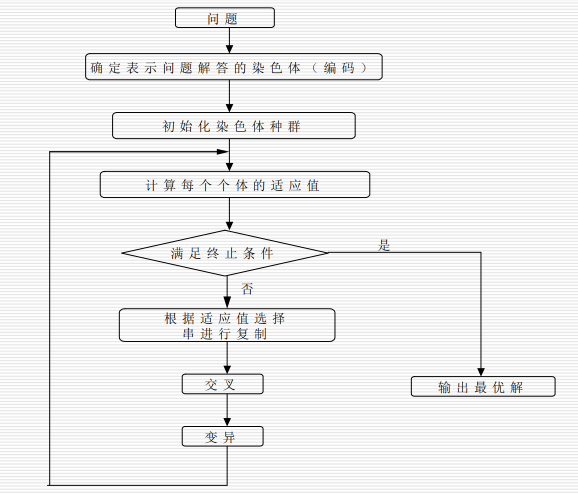
6.2 基本遗传算法:
一类借鉴生物界自然选择和自然遗传机制的随机搜索算法,非常适用于处理传统搜索方法难以解决的复杂和非线性
优化问题。
6.2.1 编码:

6.2.2 群体设定:
6.2.2.1 初始种群:
随机产生群体规模数目的个体作为初始群体。
6.2.2.2 群体规模:
群体规模太小,遗传算法的优化性能不太好,易陷入局部最优解。
6.2.2.3 适应度函数:

6.2.3 选择:
选择操作也称为复制(reproduction)操作:从当前群体中按照一定概率选出优良的个体,使它们有机
会作为父代繁殖下一代子孙。
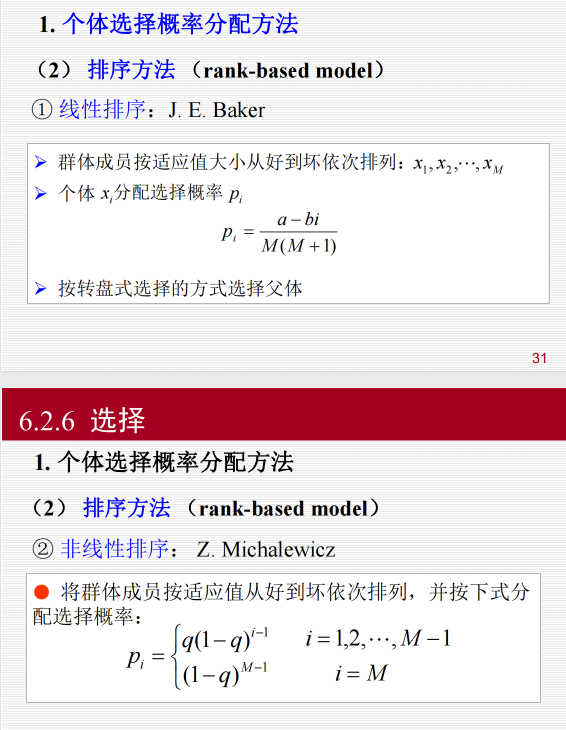
6.2.4 交叉:

6.2.5 变异:

6.3 应用举例:解决TSP问题:
问题描述:假设有一个旅行商人要拜访N个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
旅行商人问题(Traveling Salesman Problem, TSP)是一个经典的组合优化问题,它要求找到一条最短的路径,使得旅行者访问每个城市恰好一次后返回到起始城市。遗传算法是一种模拟自然选择过程的启发式搜索算法,常用于解决此类问题。
以下是实现遗传算法求解TSP问题的基本步骤:
初始化种群:随机生成一组可能的路径作为初始种群。
适应度计算:计算每个个体(路径)的适应度,适应度通常是路径长度的倒数,即越短的路径适应度越高。
选择:根据适应度从种群中选择个体,用于生成下一代。通常使用轮盘赌或锦标赛选择等方法。
交叉:从选中的个体中随机选择两个进行交叉操作,产生新的后代。对于TSP问题,常用的交叉操作有顺序交叉(OX)、部分映射交叉(PMX)等。
变异:对后代进行变异操作,以保持种群多样性。变异可以是随机交换路径中的两个城市,或者更复杂的操作。
新一代种群:根据交叉和变异产生的后代,结合一定比例的父代个体,形成新一代种群。
终止条件:如果达到最大迭代次数或解的质量达到预设阈值,则停止迭代。
输出最优解:从当前种群中选择适应度最高的个体作为问题的最优解。
下面是一个简化的遗传算法伪代码,用于求解TSP问题:
def initialize_population(size, cities):
# 初始化种群
return [random_permutation(cities) for _ in range(size)]
def fitness(individual, cities):
# 计算个体的适应度
return 1 / calculate_path_length(individual, cities)
def select(population, fitnesses):
# 选择操作
return tournament_selection(population, fitnesses, k=3)
def crossover(parent1, parent2):
# 交叉操作
return order_crossover(parent1, parent2)
def mutate(individual, mutation_rate):
# 变异操作
return swap_mutation(individual, mutation_rate)
def genetic_algorithm(cities, population_size, mutation_rate, generations):
population = initialize_population(population_size, cities)
best_solution = None
best_fitness = float('-inf')
for generation in range(generations):
fitnesses = [fitness(individual, cities) for individual in population]
next_population = []
for _ in range(len(population) // 2):
parent1, parent2 = select(population, fitnesses)
child1, child2 = crossover(parent1, parent2)
next_population.extend([mutate(child1, mutation_rate), mutate(child2, mutation_rate)])
population = next_population
current_best = max(population, key=lambda x: fitness(x, cities))
if fitness(current_best, cities) > best_fitness:
best_solution, best_fitness = current_best, fitness(current_best, cities)
return best_solution, best_fitness
# 辅助函数:计算路径长度、随机排列、轮盘赌选择、锦标赛选择、顺序交叉、交换变异等
# ...
# 使用遗传算法求解TSP问题
cities = [...] # 城市列表
best_path, best_length = genetic_algorithm(cities, population_size=50, mutation_rate=0.01, generations=100)
print("Best Path:", best_path)
print("Best Length:", best_length)请注意,上述伪代码仅提供了遗传算法的基本框架,实际实现时还需要编写辅助函数来完成具体的操作,如计算路径长度、随机生成初始路径、执行交叉和变异等。此外,遗传算法的参数(如种群大小、交叉率、变异率、迭代次数等)需要根据具体问题进行调整以获得最佳性能。
7.专家系统:
7.1 介绍:
专家系统是一种智能的计算机程序,它运用知识和推理来解决只有专家才能解决的复杂问题。
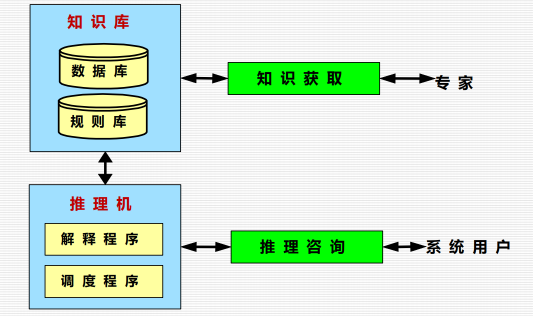
特点:
具有专家水平的专业知识
能进行有效的推理
具有启发性
具有灵活性
具有透明性
具有交互性
7.1.1 与传统程序的比较:

7.2 工作原理:
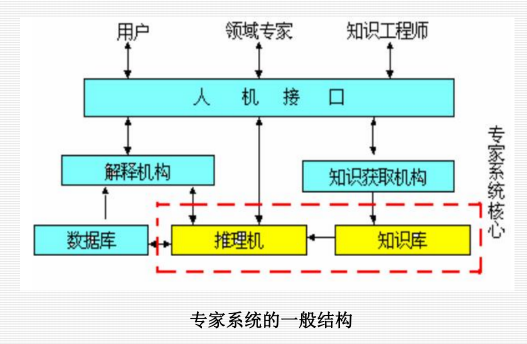
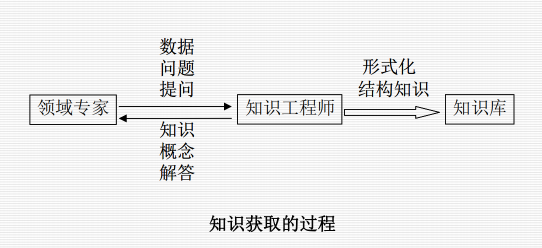
7.3 知识获取的主要过程与模式:
抽取知识、知识的转换、知识的输入、知识的检测。
8.模式识别系统:
8.1 基本概念:
8.1.1 模式:
模式:通过对具体的个别事物进行观测所得到的具有一定时间或空间分布的信息。
8.1.2 模式识别:
是指计算机将某一模式进行分类、聚类或回归分析;是研究人类识别能力的数学模型,并借助于计算机技术实现对
其模拟的科学。
8.2 系统:
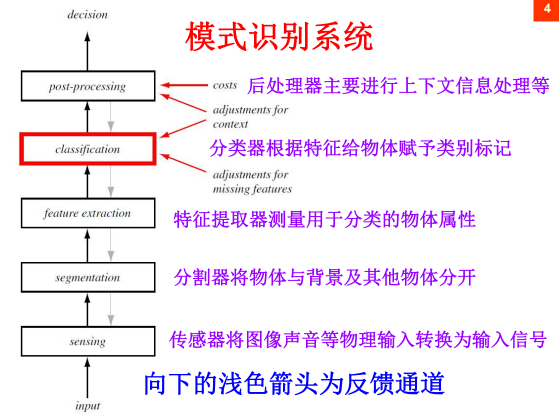
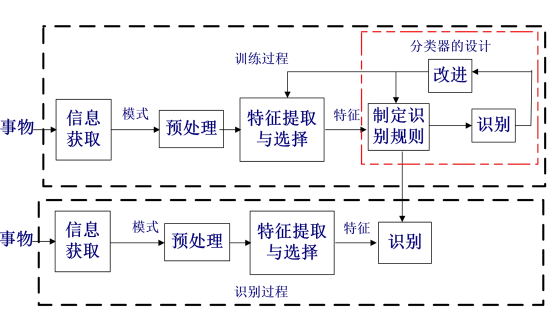
9.模型评估方法:
9.1 机器学习定理:
没有免费的午餐:没有天生优越的分类器
丑小鸭定理:没有天生优越的特征
奥卡姆剃刀:原理不要选用比“必要”更复杂的模型
9.2 经验误差与过拟合:
经验误差:模型在训练集上的误差
泛化误差:模型在测试集上的误差
9.3 模型评估方法:

9.3.1 留出法:

9.3.2 交叉验证法:

9.3.3 自助法:

9.4 模型性能度量:
9.4.1 准确率与错误率:

9.4.2 查准率与查全率:


10.机器学习模型类型:
10.1 有监督学习:
K最近邻(k-Nearest Neighbor,KNN),是一种常用于分类的算法,是有成熟理论支撑的、较为简单的经典机器学习算法之一。
基本思路:如果一个待分类样本在特征空间中的k个最相似(即特征空间中K近邻)的样本中的大多数属于某一个类
别,则该样本也属于这个类别。即近朱者赤,近墨者黑。
需要样本标签的支持,是一种有监督学习算法。

10.2 无监督学习:
k-means算法是一种简单的迭代型聚类算法,采用距离作为相似性指标,从而发现给定数据集中的K个类,且每个
类的中心是根据类中所有值的均值得到,每个类用聚类中心来描述。聚类优化目标函数。
10.3 半监督学习:
只有少量样本带标签
更符合实际需求
10.4 强化学习:

单步没有标签
流程走完时有标签
常用于游戏等人工智能应用中
10.5 自监督学习:
11.线性模型与非线性拓展:
11.1 机器学习的基本流程:

11.2 回归与分类:
回归问题的输出是连续值
分类问题的输出是离散值
区别:模型最后一层的设计方式不同
11.3 线性回归:

12.人工神经网络及其应用:
12.1 神经元与神经网络:
12.1.1 神经元模型:
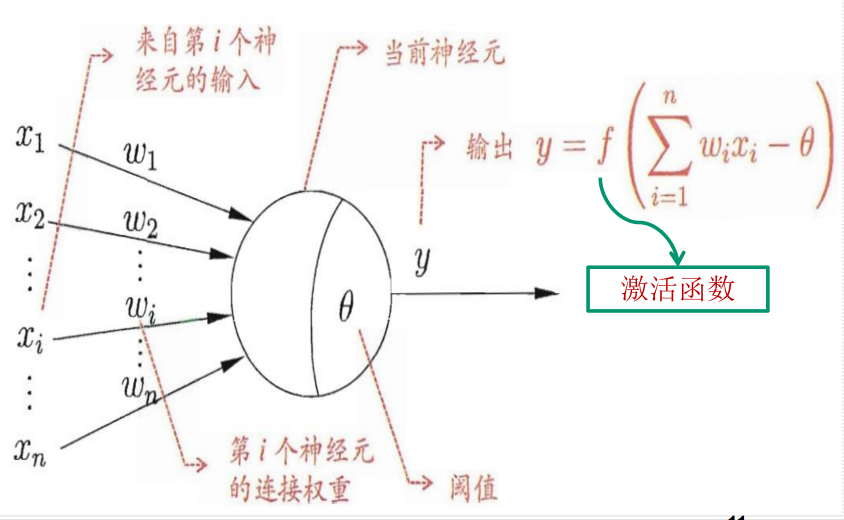
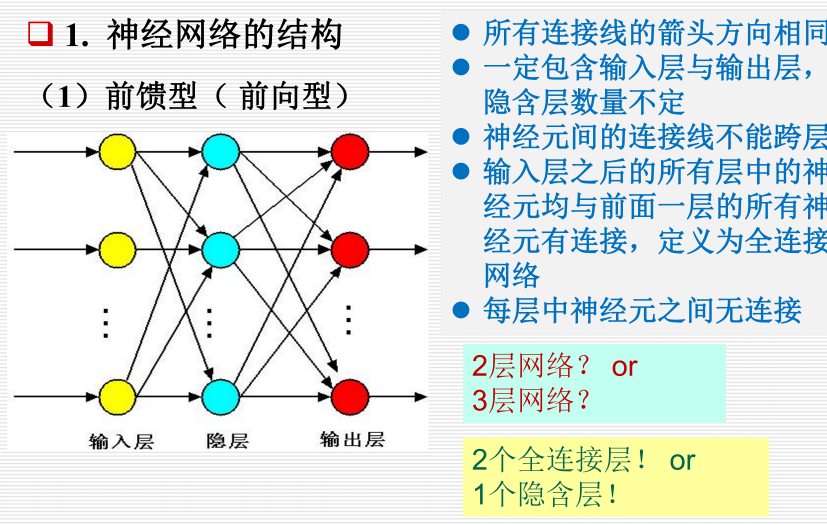
12.1.2 神经网络的结构:
前馈型:
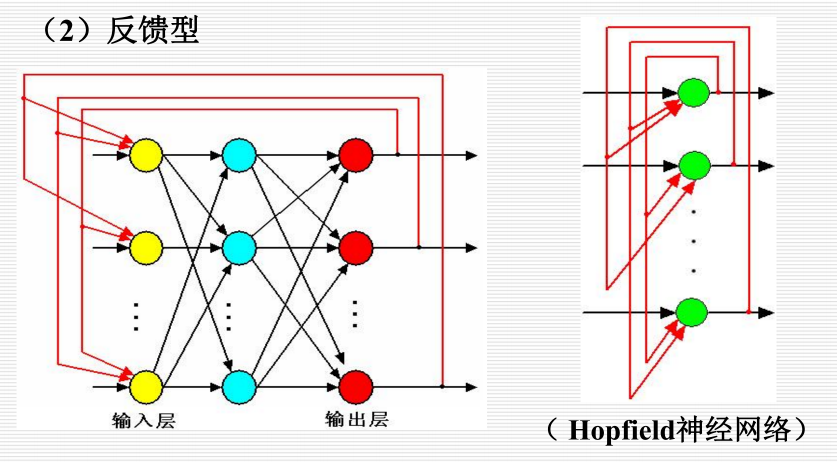
反馈型:
12.1.3 工作过程:

12.1.4 学习:
神经网络知识表示是一种隐式的表示方法。
神经网络方法是一种知识表示方法和推理方法。
1944年赫布(Hebb)提出了改变神经元连接强度的Hebb学习规则。
Hebb学习规则:当某一突触两端的神经元同时处于兴奋状态,那么该连接的权值应该增强
12.2 BP神经网络:
12.2.1 结构:
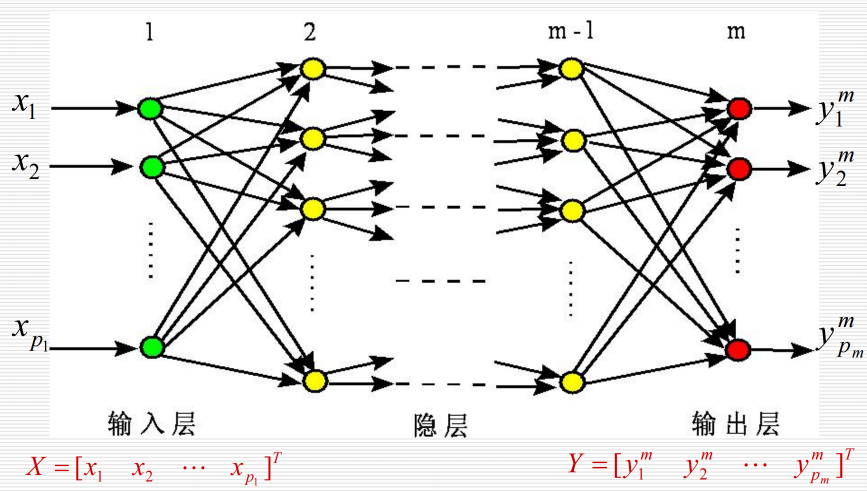
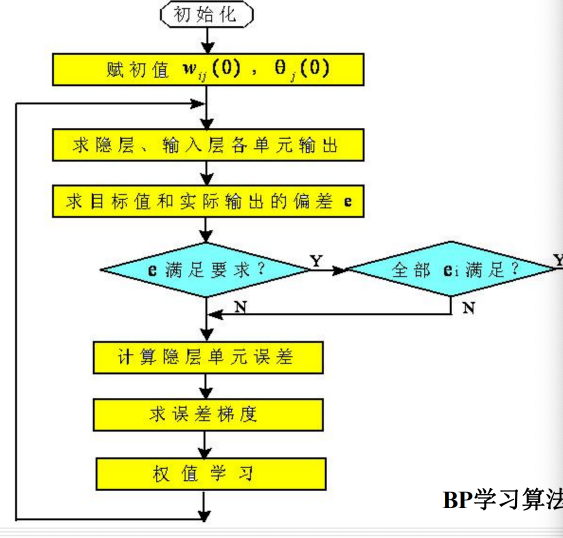
12.2.2 工作过程:

12.2.3 算法:
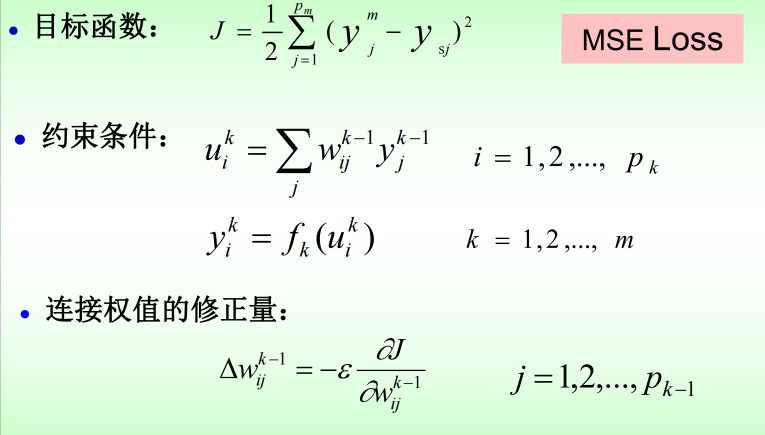
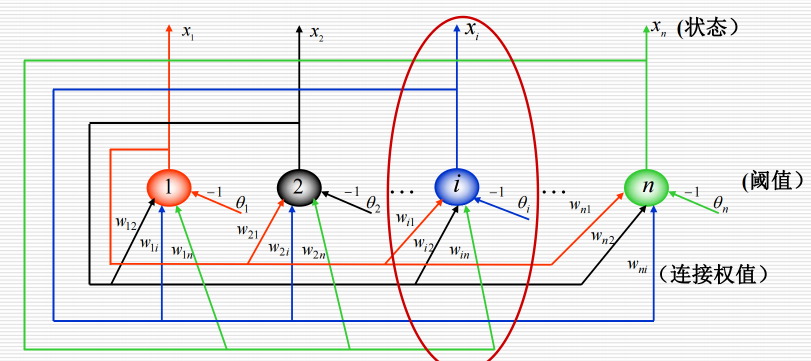
12.3 离散Hopfield 神经网络:
12.3.1 结构:
12.3.2 工作过程:

12.4 卷积神经网络:
模型通过重复的卷积层自底向上地捕捉图像特征,并根据特征进行分类。其中,池化层用于降低采样数,将一个邻域的极值(一般是最大值)取出用于代表区域特征。
12.4.1 结构:
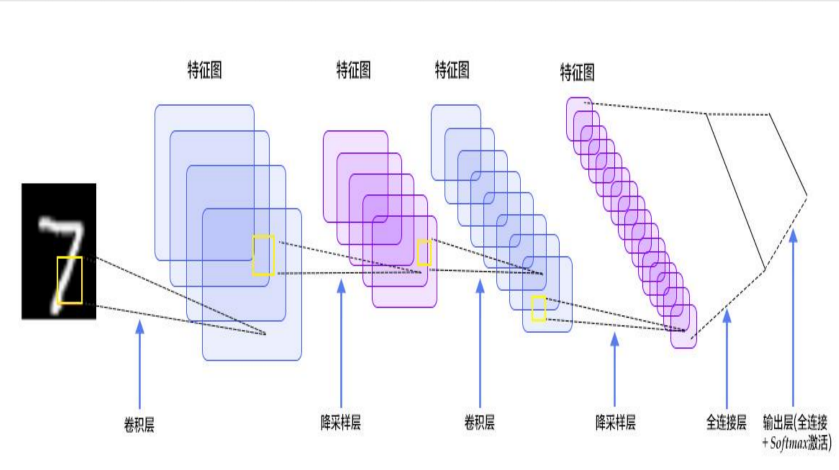
CNN是一个多层的神经网络,每层由多个二维平面组成,而每个平面由多个独立神经元组成。
C层为特征提取层(卷积层),一个卷积模板(滤波器)产生一个特征图
S层是特征映射层(池化层(Pooling)/下采样层)(可选)
每一个C层一般都紧跟着一个S层。
12.4.1.1 卷积层:
大部分的特征提取都依赖于卷积运算,利用卷积算子对图像进行滤波,可以得到显著的边缘特征。
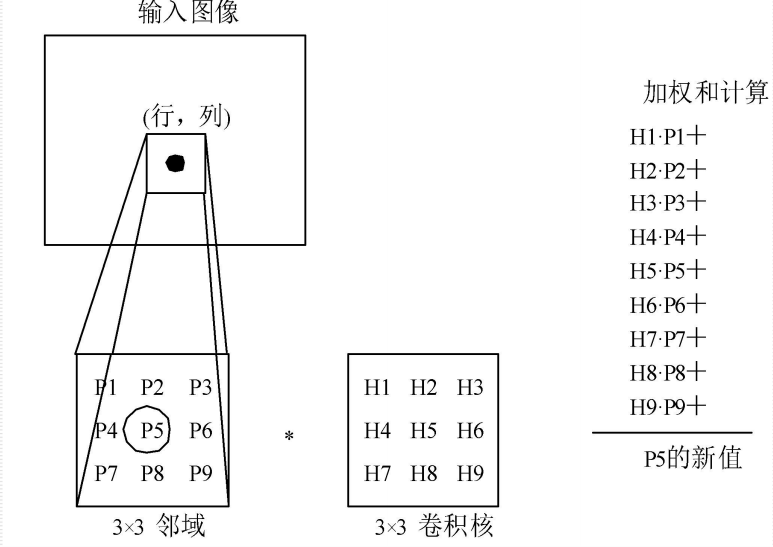
卷积核参数:

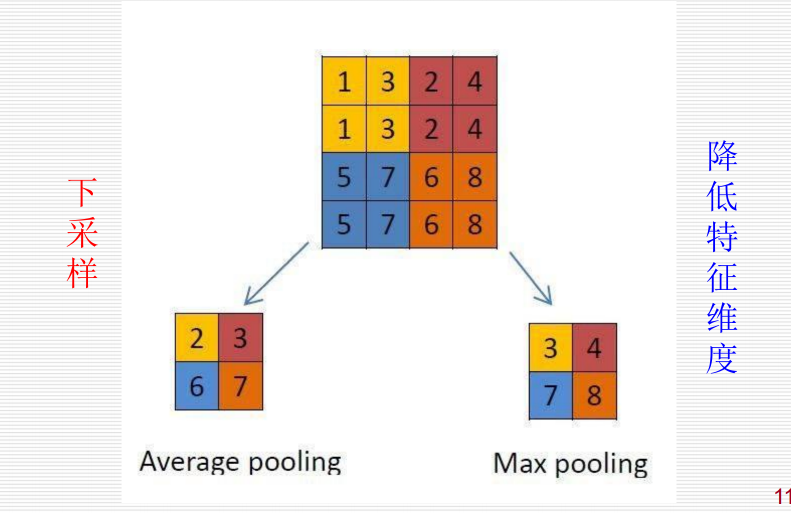
12.4.1.2 池化层:
通过卷积获得了特征之后,如果直接利用这些特征训练分类器,计算量是非常大的。
对不同位置的特征进行聚合统计,称为池化(pooling)。
卷积神经网络在池化层会丢失大的信息,从而降低了空间分辨率,导致了对于输入微小的变化,其输出几乎是不变的。
12.4.2 缺陷:
CNN中没有可用的空间信息:
CNN不会识别特征之间的相互关系。没有学习到一种正确的特征间相位置对关系(特征的姿态信息)。
池化操作导致信息严重丢失:
如最大池化,只保留最为活跃的神经元,传递到下一层,导致有价值的空间信息丢失。
12.5 胶囊网络:

12.6 生成对抗网络:
12.6.1 生成网络:
生成网络从隐空间(latent space)中随机采样作为输入,其输出结果需要尽量模仿训练集中的真实样本。
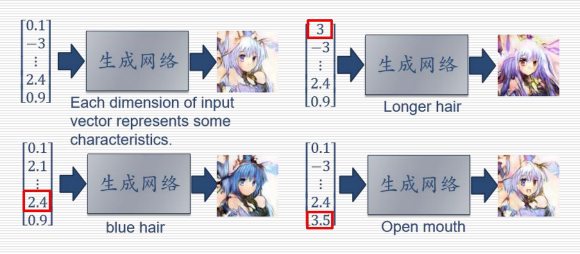
12.6.2 判别网络:
判别网络的输入则为真实样本或生成网络的输出,其目的是将生成网络的输出从真实样本中尽可能分辨出来。
12.6.3 对抗训练:
生成网络要尽可能地欺骗判别网络
判别网络将生成网络生成的样本与真实样本尽可能区分出来


